【一】期权估价原理
一、复制原理
复制原理的基本思想是:构造一个股票和借款的适当组合,使得无论股价如何变动,投资组合的损益都与期权相同,那么创建该投资组合的成本就是期权的价值。
现金流相同,价值相同?
【例】假设ABC公司的股票现在的市价为50元。有1股以该股票为标的资产的看涨期权,执行价格为52.08元。到期时间是6个月。6个月后股价有两种可能:上升33.33%,或者降低25%。无风险利率为每年4%。
1、确定6个月后可能的股票价格
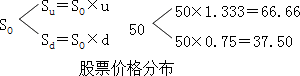
S0表示当前股票价格,Su表示上升后的股价,Sd表示下降后的股价,u为股价上行乘数,d为股价下行乘数。
上行乘数u=1+上升百分比
下行乘数d=1-下降百分比
2、确定看涨期权的到期日价值
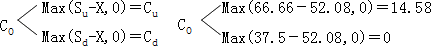
【公式推导】
构造一个股票和借款的适当组合,设借款数额为B,股票的数量为H。
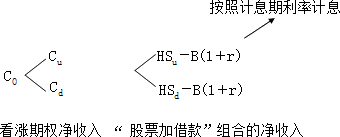
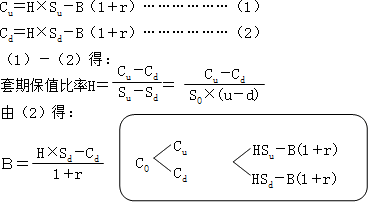
期权的价值=该投资组合成本=购买股票的支出-借款=HS0-B
这里投资组合的成本,就是投资者构造该组合的现金付出。
【说明】在股价下行时看涨期权不被执行的情况下,
借款=(到期日下行股价×套期保值比率)/(1+无风险利率)
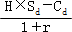
*复制组合原理计算期权价值的基本步骤(针对看涨期权)
(1)确定可能的到期日股票价格
(2)根据执行价格计算确定到期日期权价值
(3)计算套期保值比率
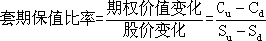
(4)计算投资组合成本(期权价值)
购买股票支出=套期保值率×股票现价=H×S0

期权价值=投资组合成本=购买股票支出-借款=HS0-B
二、风险中性原理
所谓风险中性原理是指:假设投资者对待风险的态度是中性的,所有证券的预期收益率都应当是无风险利率。风险中性的投资者不需要额外的收益补偿其承担的风险。在风险中性的世界里,将期望值用无风险利率折现,可以获得现金流量的现值。
在这种情况下,期望报酬率应符合下列公式:
期望报酬率=无风险利率=(上行概率×上行时收益率)+(下行概率×下行时收益率)
假设股票不派发红利,股票价格的上升百分比就是股票投资的收益率,股价下降的百分比就是“-收益率”。因此:期望报酬率=无风险利率=上行概率×股价上升百分比+下行概率×(-股价下降百分比)
【公式推导】
假设上行概率为P,则下行概率为1-P,于是有:
r=P×(u-1)+(1-P)×(d-1)
解之得:
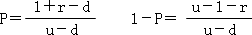
有了概率之后,即可计算期权到期日价值的期望值,然后,使用无风险利率折现,就可以求出期权的现值。
风险中性原理计算期权价值的基本步骤(假设股票不派发红利):
1.确定可能的到期日股票价格
2.根据执行价格计算确定到期日期权价值
3.计算上行概率和下行概率
【方法一】
期望报酬率=上行概率×股价上升百分比+下行概率×(-股价下降百分比)=无风险利率
【方法二】
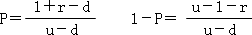
4.计算期权价值
期权价值=(上行概率×上行时的到期日价值+下行概率×下行时的到期日价值)/(1+r)
【二】二叉树期权定价模型
一、单期二叉树模型
关于单期二叉树模型,其计算结果与前面介绍的复制组合原理和风险中性原理是一样的。
以风险中性原理为例:
二、两期二叉树模型
如果把单期二叉树模型的到期时间分割成两部分,就形成了两期二叉树模型。由单期模型向两期模型的扩展,不过是单期模型的两次应用。
三、多期二叉树模型
原理:从原理上看,与两期模型一样,从后向前逐级推进
乘数确定:期数增加以后带来的主要问题是股价上升与下降的百分比如何确定问题。期数增加以后,要调整价格变化的升降幅度,以保证年收益率的标准差不变。把年收益率标准差和升降百分比联系起来的公式是:
u=1+上升百分比=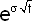
d=1-下降百分比=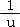
其中:e=自然常数,约等于2.7183
σ=标的资产连续复利收益率的标准差
t=以年表示的时间长度(每期时间长度用年表示)
做题程序:
(1)根据标准差和每期时间间隔确定每期股价变动乘数(应用上述的两个公式)
(2)建立股票价格二叉树模型
(3)根据股票价格二叉树和执行价格,构建期权价值的二叉树。
构建顺序由后向前,逐级推进。——复制组合定价或者风险中性定价。
(4)确定期权的现值
【三】布莱克—斯科尔斯期权定价模型
一、布莱克—斯科尔斯期权定价模型假设
(1)在期权寿命期内,买方期权标的股票不发放股利,也不做其他分配;
(2)股票或期权的买卖没有交易成本;
(3)短期的无风险利率是已知的,并且在期权寿命期内保持不变;
(4)任何证券购买者能以短期的无风险利率借得任何数量的资金;
(5)允许卖空,卖空者将立即得到卖空股票当天价格的资金;
(6)看涨期权只能在到期日执行;
(7)所有者证券交易都是连续发生的,股票价格随机游走。
二、布莱克—斯科尔斯期权定价模型
布莱克—斯科尔斯期权定价模型的公式如下:

【例·计算题】2010年8月15日,甲公司股票价格为每股20元, 以甲公司股票为标的的代号为甲20的看涨期权的收盘价格为每股1.5元,甲20表示此项看涨期权的行权价格为每股20元 。截至2010年8月15日,看涨期权还有3个月到期。甲公司股票回报率的标准差为0.4,按照连续复利计算的无风险收益率为年利率12%。
(1)使用布莱克-斯科尔斯模型计算该项期权的价值(d1和d2的计算结
转载请注明:八度生活 » 注会财务管理第九章第二节 期权价值评估的方法