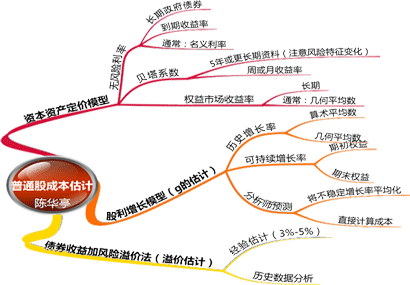
三种模型
【一】资本资产定价模型
一、基本公式
KS＝Rf＋β×（Rm－Rf）
式中：Rf—无风险报酬率
β—-该股票的贝塔系数
Rm—平均风险股票的报酬率
（Rm-Rf）—-权益市场风险溢价
β×（Rm-Rf）—-该股票的风险溢价
例：市场无风险报酬率为10%，平均风险股票报酬率14%，某公司普通股β值为1.2。普通股的成本为Ks=10%+1.2*(14%-10%)=14.8%
参数：（1）无风险利率；（2）贝塔值；（3）市场风险溢价。
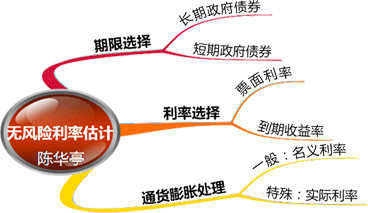
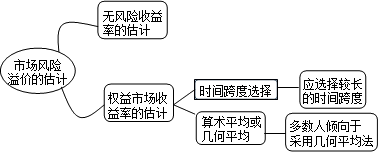
二、无风险利率估计
通常认为，政府债券没有违约风险，可以代表无风险利率。但是在具体操作时会遇到以下三个问题需要解决：
（1）如何选择债券的期限；（2）如何选择利率；（3）如何选择通货膨胀问题。
1、政府债券期限的选择
选择：通常认为，在计算公司资本成本时选择长期政府债券比较适宜。（最常见的做法，是选用10年期的财政部债券利率作为无风险利率的代表，也有人主张使用更长时间的政府债券利率）
原因：（1）普通股是长期的有价证券。从理论上分析，期限的选择应当与被讨论的现金流期限匹配。普通股的现金流是永续的，很难找到永续债券。这涉及到实务中的信息可得性。政府长期债券期限长，比较接近普通股的现金流。（2）资本预算涉及的时间长。计算资本成本的目的主要是作为长期投资的折现率。长期政府债券的期限和投资项目现金流持续时间能较好的配合。（3）长期政府债券的利率波动较小。
2、选择票面利率或到期收益率
选择：应当选择上市交易的政府长期债券的到期收益率作为无风险利率的代表。
原因：不同时间发行的长期政府债券，其票面利率不同，有时相差较大。长期政府债券的付息期不同，有半年期或一年期等，还有到期一次还本付息的，因此，票面利率是不适宜的。不同年份发行的、票面利率和计息期不等的上市债券，根据当前市价和未来现金流计算的到期收益率只有很小差别。
3、选择名义利率或实际利率
（1）相关概念及其关系
名义利率：是指包含了通货膨胀的利率。
实际利率：实际利率是指排除了通货膨胀因素的利率。
两者关系可表达如下：1+R（名义）=（1+R（实际））（1+通货膨胀率）
1+名义利率=（1+实际利率）（1+通货膨胀率）
实际现金流量：如果企业对未来现金流量的预测是基于预算年度的价格水平，并消除了通货膨胀的影响，那么这种现金流量称为实际现金流量。
名义现金流量：包含了通货膨胀影响的现金流量，称为名义现金流量。
两者的关系为：名义现金流量=实际现金流量*（1+通货膨胀率）n
（2）决策分析的基本原则
名义现金流量要使用名义折现率进行折现，实际现金流量要使用实际折现率进行折现。
（3）名义利率或实际利率的选择
实务中的做法：通常在实务中这样处理，一般情况下使用名义货币编制预计财务报表并确定现金流量，与此同时，使用名义的无风险利率计算资本成本。
特殊情况：只有在以下两种情况下，才使用实际利率计算资本成本。（1）存在恶性的通货膨胀（通货膨胀率已经达到两位数），最好使用实际现金流量和实际利率；（2）预测周期特别长，例如核电站投资等，通货膨胀的积累影响巨大。
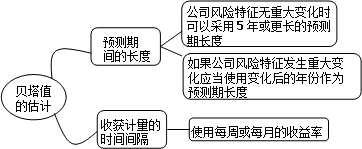
三、贝塔值的估计
1、计算方法
两种方法：一是回归直线法；二是定义公式法。
提示：两种方法均是建立在历史资料的基础之上的。涉及两个问题：（1）选择有关预测期间的长度；（2）选择收益计量的时间间隔。
2、选择有关预测期间的长度
（1）选择：公司风险特征无重大变化时，可以采用5年或更长的预测期长度；如果公司风险特征发生重大变化，应当使用变化后的年份作为预测期长度。（2）原因：较长的期限可以提供较多的数据，得到的贝塔值更具代表性，但在这段时间里公司本身的风险特征可以回发生变化。
3、选择收益计量的时间间隔
（1）选择：选择使用每周或每月的收益率
（2）原因：使用每日内的收益率会由于有些日子没有成交或者停牌，该期间的收益率为0，由此引起的偏差会降低股票收益率与市场收益率之间的相关性，也会降低该股票的β值。
使用每周或每月的收益率能显著地降低这种偏差，因此被广泛采用。
年度收益率较少采用，回归分析需要使用很多年的数据，在此期间资本市场和企业都发生了很大变化。
4、其他关注点
驱动β系数关键的因素有经营杠杆、财务杠杆和收益的周期性。如果公司在这三方面没有显著改变，就可以用历史的贝塔值估计权益成本。
提示：收益周期性是指一个公司的收入和利润对整个经济周期状态的依懒性强弱。
四、市场风险溢价的估计
含义：市场风险溢价，通常被定义为在一个相当长的历史时期里，权益市场平均收益率与无风险资产平均收益率之间的差异。
提示：前面已经解决了无风险资产收益的估计问题，因此剩下的只是权益市场平均收益率的估计。
权益市场收益率的估计：估计权益市场收益率最常见的方法是进行历史数据分析。在分析时会碰到两个问题：
（1）选择时间跨度。由于股票收益率非常复杂多变，影响因素很多，因此较短的期间所提供的风险溢价比较极端，无法反映平均水平，因此应选择较长的时间跨度。既包括经济繁荣时期，也包括经济衰退时期。
（2）权益市场平均收益率选择算术平均数还是几何平
均数。两种方法算出的风险溢价有很大的差异。多数人倾向于采用几何平均法。几何平均法得出的预期风险溢价，一般情况下比算术平均法要低一些。
例：时间 价格指数 市场收益率
0 2500
1 4000 （4000-2500）/2500=60%
2 3000 （3000-4000）/4000=-25%
算术平均收益率=（60%+（-25%））/2=17.5%
几何平均收益率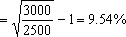
=根号3000/2500=9.54%
【二】股利增长模型
计算公式：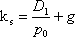
式中：KS——普通股成本
D1——预期年股利额
P0—– 普通股当前市价
g—-普通股股利年增长率
参数估计：如果一家企业在支付股利，那么D0就是已知的，而D1=D0(1+g），所以使用股利增长模型下困难在于估计股利的增长率。
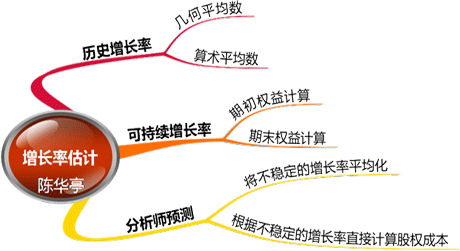
普通股利年增长率的估计方法：（1）历史增长率；（2）可持续增长率；（3）采用证券分析师的预测。
增长率估计方法：
（1）历史增长率
根据过去的股利支付数据估计未来的股利增长率，股利增长率可以按几何平均数计算，也可以按算术平均数计算。
提示：几何增长率适合投资者在整个期间长期持有股票的情况，而算术平均数适合在某一段时间
有股票的情况。由于股利模型的增长率，需要长期的平均增长率，几何增长率更符合逻辑。
例：2001-2005的股利支付情况见表
年份 2001 2002 2003 2004 2005
股利 0.16 0.19 0.20 0.22 0.25
几何增长率=根号4次方0.25/0.16-1=11.8%
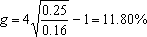
算术增长率=(（0.19-0.16）/0.16+(0.2-0.19)/0.19+(0.22-0.2)/0.2+(0.25-0.22)/0.22)/4
=11.91%
（2）可持续增长率
假设未来不发行新股，并保持当前的经营效率和财务政策不变，则可根据可持续增长率来确定股利的增长率。
股利增长率=可以持续增长率=净利润/收入*收入/资产*资产/期初权益*收益留存比率
=期初权益预期净利率*收益留存比率
按期末股东权益计算可持续增长率
股利增长率=可持续增长率=权益净利率*收益留存率/（1-权益净利率*收益留存率）
（3）采用证券分析师的预测
估计增长率时，可以将不同分析师的预测值进行汇总，并求其平均值，在计算平均值时，可以给权威性较强的机构以较大的权重，而其他机构预测值给以较小的权重。
证券分析师发布的各公司增长率预测值，通常是分年度或季度的，而不是一个唯一的长期增长率。对此，有两种处理办法：
方法：将不稳定的增长率长期化、根据不均匀的增长率直接计算股权成本。
1、将不稳定的增长率长期化；
转换的方法计算未来足够长期间（例如30年或50年）的年度增长率的几何平均数。
基期股利*（1+增长率）n=n期的股利，假设增长率是固定的。
2、根据不均匀的增长率直接计算股权成本。
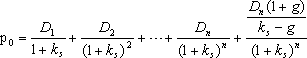
也就是每年的股利折现=P0，再用内插法算Ks
总结：
以上三种增长率的估计方法中，采用分析师的预测增长率可能是最好的办法，投资者在为股票估价时也经常采用它作为增长率。
【三】债券收益加风险溢价法
根据投资“风险越大，要求的报酬率越高”原理，普通股股东对企业的投资风险大于债券投资者，因为会在债券投资者要求的收益率上要求一定的风险溢价。依据这一理论，权益的成本公式为：Ks=Kdt+RPc
式中Kdt—-税后债务成本
RPc—–股东比债权人承担更大风险所要求的风险溢价。
参数估计：风险溢价
风险溢价估计方法：
经验估计：一般认为，某企业普通股风险溢价对其自己发行的债券来讲，大约在3%–5%之间。对风险较高的股票用5%，风险较低的股票用3%。
历史数据分析：比较过去不同年份的权益收益率和债务收益率，通常在比较时会发现，虽然权益收益率有较大波动，但两者的差额相当稳定。
转载请注明：八度生活 » 注会财务管理第六章 第二节普通股成本