【一】货币时间价值基础知识
含义:货币时间价值是指货币经历一定时间的投资和再投资所增加的价值,也称为资金时间价值。
表示方式:在实务中,人们习惯使用相对数字表示,即用增加的价值占投入货币的百分数来表示。
终值和现值的概念:1、终值又称将来值,是现在一定量现金在未来某一时点上的价值,俗称“本利和”,通常记作F。2、现值,是指未来某一时点上的一定量现金折合到现在的价值,俗称“本金”,通常记作P。
利息计算方法:单利:只对本金计算利息。复利:不仅要对本金计算利息,而且对前期的利息也要计算利息。
【二】一次性款项的现值和终值
1、单利终值与现值:
(1)单利终值:F=P+P*i*n=P*(1+i*n)。
(2)单利现值的计算与终值的计算是互逆的,由终值计算现值的过程称为折现。
(3)单利现值:P=F*(1/(1+i*n))
(4)单利现值系数与单利终值系数互为倒数。
2、复利终值与现值:
(1)复利终值公式:F=P*(1+i)n,其中(1+i)n称为复利终值系数,用符号(F/P,i,n)表示。
(2)复利现值公式:P=F*(1+i)-n,其中(1+i)-n称为复利现值系数,用符号(P/F,i,n)表示。
(3)复利现值系数(P/F,i,n)与复利终值系数(F/P,i,n)互为倒数。
【三】普通年金的终值与现值
一、有关年金的相关概念
1、年金的含义,年金是指等额、定期的系列收支。具有两个特点:一是金额相等;二是时间间隔相等。
2、年金的种类,分为普通年金:每期期末发生的年金。预付年金:每期期初发生的年金。递延年金:不是从第一期期末发生的年金,而是在第二期或第二期以后每期末发生相等数额的款项。
永续年金:无期限的年金。
二、普通年金的计算
1、普通年金终值计算
F=A*(((1+i)n-1)/i)=A*(F/A,i,n),年金终值系数(F/A,i,n)
2、普通年金现值的计算
P=A*(((1-(1+i)-n)/i)=A*(P/A,i,n),年金现值系数(P/A,i,n)
3、偿债基金和资本回收额的计算
(1)偿债基金的计算
简单的说,如果是已知年金终值求年金,则属于计算偿债基金问题,即根据普通年金终值公式求解A(反向计算),这个A就是偿债基金。
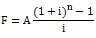
可知: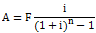
式中的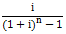 是普通年金终值系数的倒数,称偿债基金系数,记作(A/F,i,n)
是普通年金终值系数的倒数,称偿债基金系数,记作(A/F,i,n)
提示:这里注意偿债基金系数和年金终值系数是互为倒数的关系。
(2)投资回收额的计算
如果已知年金现值求年金,则属于计算投资回收额问题。即根据普通年金现值公式求解A,这个A就是投资回收额。计算公式如下:
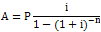 ,式中的
,式中的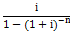 称为投资回收系数,记作(A/P,i,n)
称为投资回收系数,记作(A/P,i,n)
提示:资本回收系数与普通年金现值系数是互为倒数的关系。
总结:系数间的关系,“年终偿债”
复利终值系数与复利现值系数互为倒数
普通年金终值系数与偿债基金系数互为倒数
普通年金现值系数与投资回收系数互为倒数
【四】预付年金终值与现值
预付年金,是指每期期初等额收付的年金,又称即付年金或期初年金。有关计算包括两个方面:
1、预付年金终值的计算
即付年金的终值,是指把预付年金每个等额A都换算成第n期期末的数值,再来求和。
具体有两种方法:
方法一:F=A(F/A,i,n+1)-A=A((F/A,i,n+1)-1)
提示:预付年金终值系数与普通年金终值系数的关系:期数加1,系数减1。
方法二:预付年金终值=A(F/A,i,n)(1+i)=普通年金终值×(1+i)
2、预付年金现值的计算
具体有两种方法:
方法一:P=A(P/A,i,n-1)+A=A((P/A,i,n-1)+1)
提示:预付年金现值系数与普通年金现值系数的关系,期数减1,系数加1.
方法二:预付年金现值=普通年金现值×(1+i)=A(P/A,i,n)(1+i)
总结:
预付年金终值系数与普通年金终值系数的关系:(1)期数加1,系数减1(2)预付年金终值系数=普通年金终值系数*(1+i)
预付年金现值系数与普通年金现值系数的关系:(1)期数减1,系数加1(2)预付年金现值系数=普通年金现值系数*(1+i)
【五】递延年纪
递延年金,是指第一次等额收付发生在第二期或第二期以后的年金。
m–递延期,n–连续支付期
1、递延年金终值计算
计算递延年金终值和计算普通年金终值类似
F=A*(F/A,i,n)
注意:递延年金终值只与连续支付期n有关,与递延期m无关。
2、递延年金现值的计算
方法1:两次折现
计算公式如下:P=A*(P/A,i,n)*(P/F,i,m)
方法2:年金现值系数之差
P=A*(P/A,i,m+n)-A*(P/A,i,m)
=A*((P/A,i,m+n)-(P/A,i,m))
【六】永续年金
永续年金,是指无期限等额收付的年金。
永续年金因为没有终止期,所以只有现值没有终值。
P=A/i
【七】折现率、期间的推算
用内插法
例题:现在向银行存入20000元,问年利率i为多少时,才能保证在以后9年中每年年末可以取出4000元。
答案:
根据普通年金现值公式
20000=4000*(P/A,i,9)
(P/A,i,9)=5
查表并用内插法求解。查表找出期数为9,年金现值系数最接近5的一大一小两个系数。
(P/A,12%,9)=5.3282
(P/A,14%,9)=4.9464
利率 年金现值系数
12% 5.3282
i 5
14% 4.9464
(i-12%)/(14%-12%)=(5-5.3282)/(4.9464-5.3282)
i=13.72%
【八】报价利率、计息期利率和有效年利率—-一年内多次计息情况
1、含义
例:某种债券面值1000元,每半年付息一次,付息金额为100元。
那么计算利率
(1)100/1000=10% 半年利率 ,就是计息期利率
(2)200/1000=20% 年利率,就是报价利率(不符合复利计息原理)
(3)(100+100+10)/1000=21% 复利计算的年利率,就是有效年利率
总结:三个利率的换算
计息期利率=报价利率/年复利次数=r/m
有效年利率i=(1+r/m)m-1
根据这两个公式,可以进行利率的相互推算。比如已知计息期利率可以推算有效年利率。
有效年利率与报价利率的比较关系:当m=1时,有效年利率=报价利率;当m>1时,有效年利率>报价利率
【九】连续复利
如果每年复利次数m趋近于无穷,则这种情况下的复利称为“连
转载请注明:八度生活 » 注会财务管理第四章第一节货币时间价值